La formula delle lenti sottili afferma una relazione tra distanza focale, distanza dell’immagine e distanza dell’oggetto, in una lente.

Introduzione

Iniziamo con una situazione ideale: un bastoncino viene posato a distanza p da una lente convergente, con distanza focale f.

  • q = distanza dell’immagine {proiezione dell’oggetto}
  • p = distanza oggetto
  • f = distanza focale della lente

Questa dimostrazione proverà attraverso rapporti geometrici la formula delle lenti sottili, ossia:

\[\frac{1}{p}+\frac{1}{q}=\frac{1}{f}\]

Dimostrazione

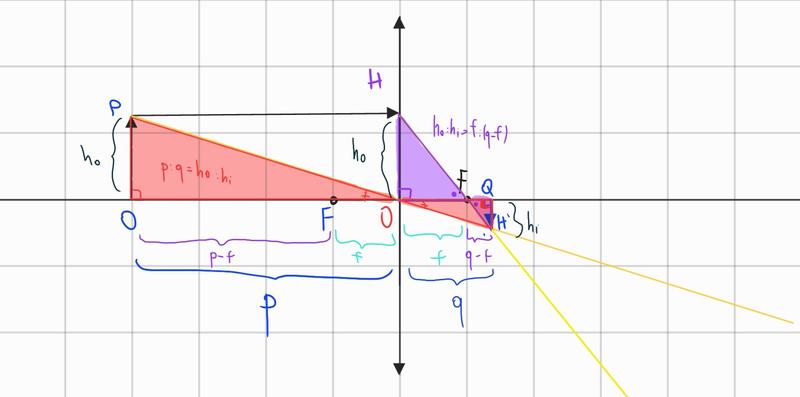
Dimostrazione grafica con disegno

Considero i triangoli HCF e FQH’, essi sono simili poiché:

  • \(F\hat{Q}H \cong F\hat{C}H' \cong \frac{\pi}{2}\) per costruzione
  • \(H\hat{F}C \cong H'\hat{F}Q\) perché opposti al vertice
  • \(C\hat{H}F \cong F\hat{H'}Q\) per differenza di angoli congruenti

Se HCF e FQH’ sono simili, allora

\[\frac{CH}{CF}=\frac{QH'}{QF} \Rightarrow \frac{h_o}{f}=\frac{h_i}{q-f}\]

Del rapporto soprastante appena ricavato dalla similitudine dei triangoli, ottengo che, l’altezza dell’oggetto sta alla distanza focale, come l’altezza dell’immagine sta alla sottrazione tra distanza dell’immagine e distanza focale. Posso semplificarlo in questo modo:

\[\frac{q-f}{h_o}*\frac{h_o}{f}=\frac{h_i}{q-f}*\frac{q-f}{h_o}\] \[\Rightarrow \frac{h_i}{h_o}=\frac{q-f}{f}\]

Successivamente considero i triangoli POC e CQH, essi sono simili poiché:

  • \(P\hat{O}C \cong C\hat{Q}H' \cong \frac{\pi}{2}\) per costruzione
  • \(O\hat{C}P \cong Q\hat{C}H'\) perché opposti al vertice
  • \(C\hat{H}Q \cong C\hat{O}P\) per differenza di angoli congruenti

Se POC e CQH sono simili, allora

\[\frac{QH'}{PO}=\frac{CQ}{OC} \Rightarrow \frac{h_i}{h_o}=\frac{q}{p}\]

Conclusione

Unendo i risultati dalla similitudine delle due coppie di triangoli, ottengo che:

\[\frac{q}{p} = \frac {q-f}{f}\]

Adesso basta soltanto eseguire delle semplificazioni per ottenere la formula delle lenti sottili.

Il metodo utilizzato qui sotto per semplificare il risultato non è quello più veloce, ma è uno dei più semplici da intuire.

$ 0 = \frac{-q+f}{f}+\frac{q}{p} $

$ 0 = \frac{1}{q}(\frac{-q}{f}+\frac{f}{f}+\frac{q}{p}) $

$ 0 = -\frac{1}{f}+\frac{f}{fq}+\frac{1}{p} $

$ \frac{1}{f} = \frac{1}{q}+\frac{1}{p} $

Come volevasi dimostrare, c.v.d.

Suggerimento: questa dimostrazione può essere utilizzata anche per verificare la formula dell’ingrandimento!