Escher e il ruolo della matematica nelle sue opere

Escher era un incisore, stampava partendo da una matrice, o un blocco di legno o pietre trattate chimicamente e lavorate a mano.

Una delle sue prime opere era la stilografia di un gatto bianco, più il legno veniva scolipito più la parte diveniva bianca. Inoltre troviamo anche una litografia, disegno sulla pietra con una matita ad olio, dove poi si mettteva un acido acquoso che si depositava sulle parti d’acqua senza olio del disegno, poi la sostanza veniva tratta chimicamente ulteriormente ed alla fine veniva steso il colore.

Era un lavoro di estrema precisione, bisognava disegnare al contrario, per incidere sulla matrice. Il suo uso della mano sinistra lo agevolava.

L’opera di Escher comprende 450 stampe diverse, con 5 tecniche diverse:

• Incisioni su linoleum (strato sottile a base di olio di lino posto su una superficie piana e levigato)

• Xilografie

• Litografie

ed altro, come diversi tipi di incisioni. Escher voleva comprendere le idee della matematica per inserirle nella sua parte, ne sapeva molto poco e quella che aveva studiato non gli piaceva. Era affascinato dalle idee matematiche che voleva rappresentare nella sua parte, alcune sue opere sono metafore visive di concetti matematici astratti, ne vedremo alcuni esempi più tardi.

In particolare, era ossessionato dall’idea di rappresentare l’infinito in una superficie chiusa, qualcosa che si spande illimitato ed irraggiungibile. Secondo suo figlio George Escher aveva lo stesso spirito di un matematico, definendo un insieme di regole con il quale studiare un ambiente nel proprio mondo astratto, portando ad importanti scoperte e risultati appaganti.

Vita in breve #

Nel 1919 entra in una scuola di architettura ad Haarlem in Olanda. Tutti i suoi fratelli erano ben avviati in campo scientifico, quindi la scienza l’ha sempre accompagnato, anche se era accompagnato dalle arti decorative.

Nel 1922 inizia a viaggiare in Italia e in Spagna, scoprendo nuovi mondi affascinanti. Il viaggio in Spagna lo porta a concepire il concetto di riempimento del piano. Una tassellazione è un modo di ricoprire il piano euclideo con una o più figure geometriche chiamate tasselli, ci sono delle regole:

• Nessuna sovrapposizione

• Nessun vuoto

Il concetto di tassellazione risale anche fino ai sumeri, con la tassellazione del tempio di Uruk (3400-3100 a.C.). Un mosaico è un esempio di tassellazione, ma l’arte araba, come il santuario di Fatima in Iran, mostrano la maestria raggiungibile nell’arte della tassellazione. L’Alhambra a Grenada, in Spagna, è meravigliosa. Escher l’ha visitata in più occasioni ed ha disegnato diverse tassellazioni arabe riproducendole sul suo tacccuino.

Il primo trattato sulle tassellazioni è di Keplero, Harmonices Mundi, risalente al 1619. Bisogna parlare del concetto di tassellazione periodica in cui ci sono due traslazioni indipendenti che mantengono invariata la tassellazione.

Come si può tassellare un piano in modo periodico? #

Teorema del cristallografo e matematico russo E.S. Fëdorov: ci sono 17 tipi di tassellazioni periodiche.

Ovunque c’è un po’di simmetria, un gruppo di simmetria interviene.

Il gruppo misura la simmetria degli oggetti. Ecco i 17 gruppi cristallografici, divisi da Polya, che in qualche modo hanno ispirato Escher. Escher fu spinto a questi studi dal fratellastro Beer, geologo, che indirizzò MCE su articoli di cristallografia di Polya, Haag e altri. Dal 1933 inizia uno scambio epistolare tra Escher e Polya. Escher è riuscito a rappresentare tutti i 17 tipi di tassellazioni periodiche.

Dal 1941 in poi, Escher inizia a tenere Il Taccuino dove studia le tassellazioni e la geometria delle figure. Usa il simbolismo matematico con aggiunte personali. Si trovano in tale taccuino anche gli studi di transizione, che cambiano l’apparenza di una tassellazione senza cambiarne il gruppo cristallografico, ottenendo una transizione fluida. In una transizione di quel tipo cambiano proprietà topologiche e combinatorie ma il gruppo resta lo stesso.

Esempio: Dag en nacht, xilografia

Nelll’opera della metamorfosi, si può osservare una striscia lunga diversi metri in cui gli uccelli in volo si trasformano e diventano case e poi le case diventano un paesaggio italiano: il paesino di Atrani sulla costrera amanlfitana che poi verte verso una scacchiera.

Escher nel 1954 ad Amstersdam, accompagnato da una mostra di stampe, disegni, sculture e linee incontra due matematici che cambieranno radicalmente la sua carriera. Penrose viene coòpito dall’immagine Relativity che ad oggi compare anche in un episodio dei Simpson ed in un film con David Bowie. Penrose elabora il triangolo di Penrose dopo aver osservato l’opera, una figura paradossale con tre barre che formano un triangolo, come il logo di Google Drive.

Escher rimane colpito dalla figura di Penrose ed elabora una nuova opera: Ascending and Descending, caratterizzata da scale infinite.

Escher voleva imprigionare l’infinito in una superficie chiusa, quindi Coxeter qualche anno dopo la mostra inviò ad Escher una copia del suo lavoro “Crystal symmetry…” ed Escher risponde alcune delle tue illustrazioni mi hanno quasi scioccato. Escher cerca di ricostruire i cerchi di raggi interni dell’illustrazione superiore ed incuriosito cerca altri metodi per costruire figure simili. Coxeter rsponde con questo disegno, con la tassellazione classficiata [3,7] in cui i numeri primi 3 e 7 giocano un ruolo significativo. Escher dopo scrive al suo figlio e sperava in un due o un quattro come artista, poiché più facile da disegnare. Scrive che ha grande entusiasmo per questa figura e ne cerca la soluzione.

Il Grafo di Farey #

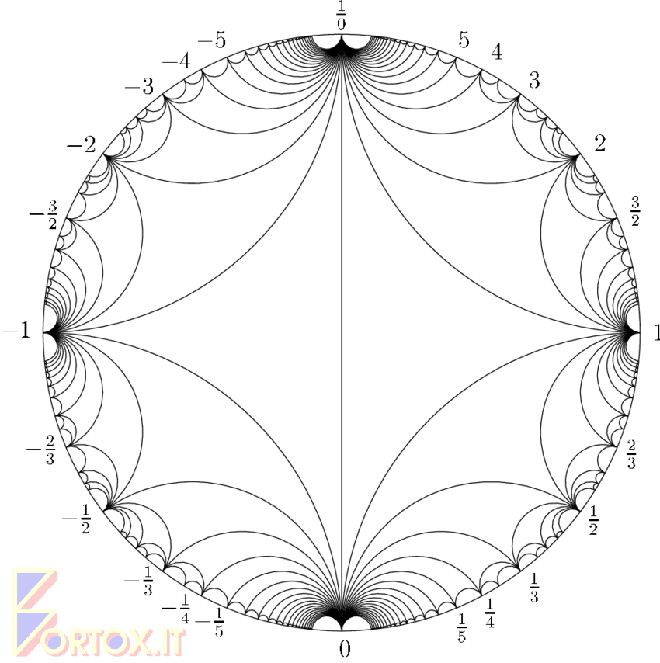
Il grafo di Farey, geologo, è costituito da infiniti triangoli curvilinei. Ogni numero razionale p/q compare come vertice di qualche triangolo nel grafo di Farey, dipende dallo sviluppo di una frazione continua. I triangoli del grafo forniscono una tassellazione completa. Escher riuscì a scoprire le regole matematiche, ad esempio nelle sue Circle Limit, nella prima la tecnica ha alcuni errori, ma nella terza e nella quarta, l’ultima, la più conosciuta che raffigura angeli demoni, la tassellazione è perfetta.

Effetto Droste #

Il disegno è un esempio di grafica ricorsiva. In mezzo si trova la firma di Escher. Nel 202 un team guidato dal matematico Lenstra ha analizzato Print Gallery. La litografia è un disegno su una curva ellittica sul campo dei numeri complessi. La curva contiene una copia di se stessa che si ripete nello spazio centrale, ruotata di 158° e scalata di 22,2. Escher aveva solo abbozzato la ripetizione, e non si riproduceva all’infinito. Si chiama Effetto Droste, quello che ha realizzato Escher, ed eredita il nome da una fabbrica di cioccolato.

Una suora tiene una scatola di cioccolato in cui l’immagine viene ripetuta all’infinito. Si trova questo effetto anche nel polittico stefaneschi di Giotto. Il team ha dapprima analizzato la griglia alla base del disegno, che è stata poi riportata su un piano euclideo, aggiustata dalle imprecisioni commesse da Escher e completata così da riprodurre l’effetto Droste ipotizzato ed abbozzato dall’artista.