- Benvenuti nel nido del cuculo/
- Compiti ed Appunti Scolastici/
- Tre leggi di Keplero, storia, utilizzi ed ellissi/
Tre leggi di Keplero, storia, utilizzi ed ellissi
Tabella dei contenuti
Questo articolo contiene:
- Introduzione matematica sulle formule dell’ellisse (le orbite dei pianeti sono ellittiche secondo le leggi di Keplero)
- Storia della vita di Johannes Kepler
- Enunciazione delle tre leggi di Keplero
Matematica delle ellissi in breve #
In un ellisse, la distanza di un punto dai due fuochi è pari ad una costante k.
Come disegnare un’ellisse: prendo una pagina di quaderno, inficco due puntine nella stessa, collego le puntine con uno spago che tengo in tensione, se metto un lapis all’estremità dello spago e lo giro ottengo un’ellisse.
La porzione di spago tra i due fuochi (le due puntine) ha avuto una lunghezza costante (k) durante il movimento del lapis sul foglio formando punti (Pn).
$$ F_1 P +F_2 P = F_2 P_1 + F_1 P_1 = k $$
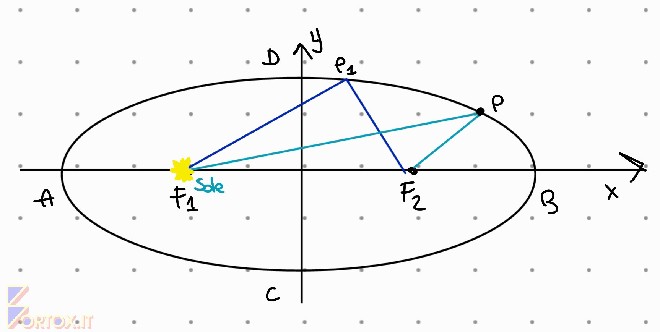
Keplero ritiene che il Sole si trovi in uno dei due fuochi e che un pianeta del Sistema Solare, ad esempio la Terra, orbiti attorno al Sole come un punto che si muove sull’ellisse.
Un ellisse è il luogo geometrico dove la distanza di un punto dai due fuochi (punti fissi) F1 ed F2 è costante –> F1P + F2P = k.
Afelio e perielio #
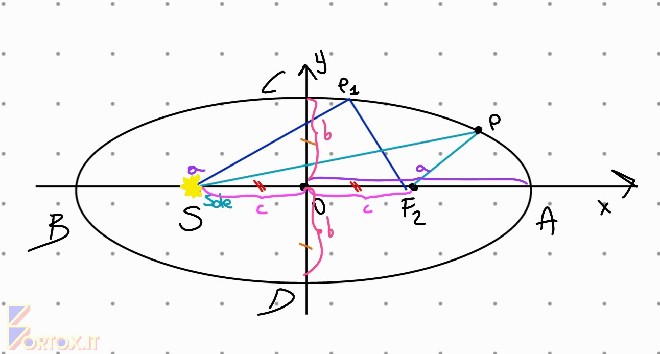
In tale ellisse - con centro nell’origine - , considero il semiasse maggiore misurare a=AO=BO=AB/2, mentre il semiasse minore misurare b=CO=DO=DC/2.
Tutte le ellissi trattate in questo documento hanno **a>b**, dunque si tratta di un **caso particolare**. Esistono anche ellissi con **b>a** e circonferenze, ossia ellissi con **b=a** ma **non è necessario** studiarle per approfondire le leggi di Keplero.La distanza tra i due fuochi F1F2 (distanza focale) è 2c., dunque la distanza tra un fuoco ed il centro dell’ellisse è 2c/2 ossia c, poiché O è il punto medio di F1F2.
| Nome | Formula |
|---|---|
| Asse maggiore | 2a |
| Asse minore | 2b |
| Semiasse maggiore | a |
| Semiasse minore | b |
| Distanza focale | 2c |
Considerando S=F1 il punto più vicino al Sole - ossia il perielio - la distanza pianeta-Sole sull’ellisse misurerà a-c ossia il semiasse maggiore meno metà distanza focale.
Invece considerando il punto sull’ellisse con maggiore distanza dal Sole, l’ afelio, la distanza pianeta-Sole misurerà a+c ossia il semiasse maggiore più metà distanza focale.
| Nome | Formula |
|---|---|
| Distanza al perielio | a-c |
| Distanza all’afelio | a+c |
Eccentricità di un’ellisse #
Considero un'ellisse con a>bPer definire rapidamente la forma di un’ellisse si usa la sua eccentricità, ossia il rapporto tra l’asse maggiore (2a) e la distanza focale (2c).
Se l’eccentricità è prossima allo zero, l’ellisse assomiglia ad una circonferenza, se invece è prossima ad uno, assomiglia ad una linea retta.
$$ e = \frac{c}{a} $$
Infatti se c misura zero, 2c corrisponde a zero, i due fuochi si sovrappongono ed ottengo una circonferenza.
![Immagine di una circonferenza con la dicitura dell’ellisse]
Se invece c è prossimo al valore di a, otterrò con c/a un valore prossimo ad uno, ed una linea retta in un disegno.
![Immagine ellisse con Geogebra con c=0.98, a=1.00]
Formule necessarie #
Considero un'ellisse con a>bQueste sono le formule che abbiamo usato nei nostri problemi a fisica, sempre considerando ellissi con a>b.
| Nome | Formula |
|---|---|
| Afelio | a+c |
| Perielio | a-c |
| Distanza focale | 2c |
| Eccentricità | c/a |
| c | \( \sqrt{a^2-b^2} \) |
Per trattare le leggi di Keplero e problemi sulle orbite dei pianeti basta sapere queste formule.
Vita di Johannes Kepler #
Johannes Kepler, Giovanni Keplero, nasce nel 1571, a Weil der Stadt, presso Stoccarda, nel ducato protestante del Wurttemberg. Nasce in una famiglia protestante.
- Nel 1577, a 6 anni, vede la Grande Cometa in un posto sopraelevato
- Nel 1580, a 9 anni, vede la Luna Rossa con il padre.
- Nel 1584, grazie alla riforma protestante, può iscriversi all’Università di Tubinga anche se da famiglia non abbiente. Viene introdotto al sistema copernicano da Michael Maestlin.
- Nel 1588, a 17 anni, il padre mercante abbandona definitivamente la famiglia.
- Nel 1594, Keplero, appassionato di Astronomia, insegna alla cattedra di Graz, ma si riduce all’esecuzione di oroscopi per guadagnarsi da vivere.
- Nel 1596 pubblica il Mysterium Cosmographicum, mistero del cosmo.
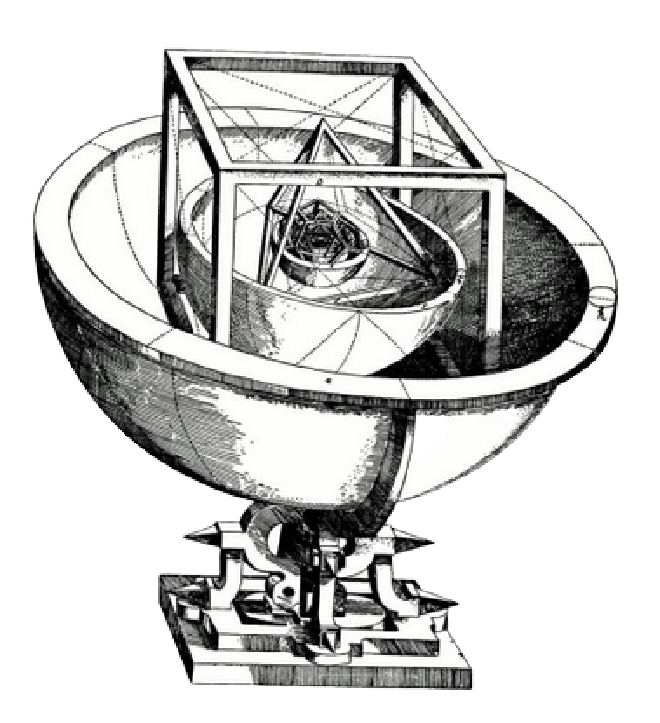
In questo libro si nota un retaggio della visione platonica dell’universo, predominante anche grazie alla diffusione della religione cristiana, infatti Keplero immagina i pianeti con la forma di solidi platonici, contenuti ognuno in una propria “sfera” più la Terra: in totale sei pianeti per l’intero Sistema Solare.
Mi sono proposto di dimostrare con questa operetta, o lettore, che Dio Ottimo Massimo, nella costruzione del mondo e nella disposizione dei cieli, guardò ai cinque corpi solidi regolari che tanto sono stati celebrati fino dal tempo di Pitagora e di Platone […]
- Keplero, Mysterium Cosmographicum
I solidi Platonici sono solidi formati da figure geometriche regolari, e sono cinque.
- Tetraedro, formato da 4 triangoli.
- Esaedro, comunemente chiamato cubo, formato da 6 quadrati.
- Ottaedro, formato da 8 triangoli.
- Dodecaedro, formato da 12 pentagoni.
- Icosaedro, formato da 20 triangoli.
- Nel 1600 si trasferisce a Praga ed affianca l’astronomo Brahe nella sua ricerca.
Keplero si trasferisce da Brahe anche per un interesse personale: Brahe aveva raccolto in oltre 30 anni di osservazione del cielo, dati approfonditi sul movimento di Marte, che non era disposto ad affidare al suo allievo Keplero.
Nel 1601 Brahe muore, Keplero si impossessa dei dati decennali di osservazioni del cosmo
Nel 1609 Keplero pubblica l’ Astronomia Nova, un trattato sul cosmo contenente le prime due leggi.
Nel 1619 Keplero pubblica l’ Harmonice Mundi, un trattato di musica in cui è contenuta la terza legge.
Il 15 novembre 1630 Keplero muore; la sua tomba viene distrutta due anni dopo durante la guerra dei trent’anni.
Un incarico come astrologo per tirare a campare e una madre accusata di stregoneria. Il vaiolo all’età di quattro anni, l’umile condizione sociale e una moglie facoltosa deceduta in preda alla pazzia. Il conflitto tra cattolici e protestanti, …., diversi figli morti troppo presto. Non è stata facile la vita per Giovanni Keplero, come probabilmente non deve essere stato facile seguire con pervicacia lo studio scientifico proprio quando la scienza appena nata metteva in discussione saperi e autorità millenarie e allo stesso tempo tutto sembrava mettersi di traverso nel privato. Questa esistenza tribolata emerge riga dopo riga nei suoi lavori che «tratteggiano, in modo spesso passionale, le vicende quotidiane, la storia del tormentato mondo in cui vive, oltre all’evoluzione del pensiero scientifico».
- A.M. Lombardi I grandi della Scienza
Le tre leggi di Keplero #
L’orbita di un pianeta è ellittica, il Sole è uno dei due fuochi.
Il raggio vettore (pianeta-sole) spazia aree uguali in tempi uguali.

- Il rapporto tra il quadrato del periodo di rivoluzione T e il cubo del semiasse maggiore a è costante per ogni pianeta.
$$ \frac{T^2}{a^3} = k $$
Una relazione sesquialtera #
Siccome l’esponente di t è 2, mentre l’esponente di a corrisponde a 3, stiamo parlando id una relazione sesquialtera. Una proporzione sesquialtera evidenzia la relazione tra le frequenze di note piacevoli all’udito se suonate contemporaneamente. Ad esempio il rapporto tra la frequenza del “SOL” e la frequenza del “DO” corrisponde a tre mezzi.
\(\frac{F_{SOL}}{F_{DO}} = \frac{3}{2}\)
Il termine sesquialtera deriva dal greco sesqui = due terzi e altera = l’altro.
Keplero non a caso pubblicò la terza legge nel 1619, dieci anni dopo la pubblicazione delle precedenti, nel trattato di musica Harmonice Mundi.
Come utlizzare la III legge nel Sistema Solare #
Se considero il Sistema Solare, le unità di misura “comode” per eseguire questo calcolo sono l’anno e l’unità astronomica, perché, considerando l’orbita della Terra, il periodo di rivoluzione terrestre è pari ad un anno, mentre la distanza Terra-Sole corrisponde esattamente ad un’unità astronomica.
$$ \frac{T^2}{a^3} = \frac{1a^2}{(1U.A.)^3} = k = 1 \frac{a^2}{(U.A.)^3} $$
Ovviamente, quando si lavora con il k ricavato sopra, ogni distanza pianeta-Sole dovrà essere convertita da km a U.A. ed ogni periodo di rivoluzione da secondi ad anni.Per tutti i pianeti orbitanti attorno al Sole, k corrisponde ad \( 1 \frac{a^2}{(U.A.)^3} \), costante molto comoda da utilizzare.
Se invece trovo una Luna che orbita attorno ad un pianeta, non posso usare \( k = 1 \frac{a^2}{(U.A.)^3} \) la Luna non orbita attorno al Sole.
k è costante per tutti gli oggetti orbitanti attorno ad un altro oggetto