Dimostrazione proporzionalità inversa tra raggio vettore e velocità pianeta

Dimostro che velocità di un oggetto e distanza dello stesso dal fuoco sono inversamente proporzionali in un’orbita ellittica sfruttando la II legge di Keplero.

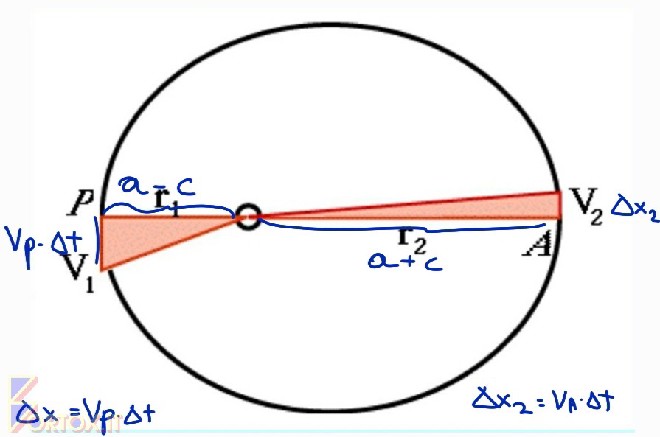
Considero due spostamenti sull’ellisse, \(\Delta X_1\) e \(\Delta X_2\).

\(\Delta X_1\) e \(\Delta X_2\) sono spostamenti molto piccoli, perciò:

• Posso utilizzare la velocità istantanea come velocità media sullo spostamento, anche se la velocità nell’intera orbita varia.

• Posso approssimare lo spostamento ad una linea retta, non ad una curva.

Siccome per la seconda legge di Keplero le aree disegnate dal raggio vettore in tempi uguali hanno area uguale, posso imporre l’uguaglianza ai prodotti tra raggi vettori e spostamenti.

$$ \frac{b * h}{2} = \frac{b * h}{2} $$

$$ \frac{\Delta X * r_P}{2} = \frac{\Delta X_1 * r_A}{2} $$

$$ v_P * \Delta t * r_P = v_A * \Delta t * r_A $$

$$ v_P * r_P = v_A * r_A $$

$$ \frac{v_P}{v_A} = \frac{r_A}{r_P} $$

q.e.d.

La proporzionalità inversa tra raggio vettore e velocità è stata dimostrata.

Vedi anche leggi di Keplero; enunciazione, utilizzo e storia